马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?加入我们

x
本帖最后由 bewarm 于 2012-10-5 11:25 编辑
警告:前方高能.有数学恐惧症者退散
然后耐心等待公式载入完毕
如果你喜欢撸弦乐器,泛音这玩意儿一定不陌生吧.
可是很多人都只知道如何操作,却不太明白为啥要按那个地方,还要虚按.
我们以吉他为例来说说这个问题.
吉他从本质上来讲就是六根两端固定的弹性弦
我们取其中一根来研究.
当然我们需要用拨片拨一下才会有声音(玩指弹的不要吐槽我!
于是吉他的状态就变成了这样(当然没有图示的这么夸张,这样弦早就断了,就算25一套的达达里奥你也伤不起啊

数学化的描述就是:
设弦的振幅为) ,于是初始状态为 ,于是初始状态为
=\\begin{cases}\\frac{h}{x_0}x%20&%200%3Cx%3Cx_0%20\\\\\\frac{h}{l-x_0}(l-x)%20&%20x_0%3Cx%3Cl\\end{cases})
拨片松开之后弦就开始振动了,注意这时,弦已经不是像初始状态那样的线性分布了.
所以需要取一小段微元做受力分析,以为可以看成是直线的存在.
这段弦原长 ,拨动后左端偏移了 ,拨动后左端偏移了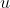 ,右端偏移了 ,右端偏移了

这段弦两端受到拉力) 和 和) ,产生了加速度 ,产生了加速度
根据牛顿第二定律有
-\\mathbf{T}(x)=\\int_x^{x+\\Delta%C2%A0x}\\rho(x)\\mathbf{a}dx)
其中 是弦的密度,至于右边的那个积分其实就是简单的质量乘以加速度 是弦的密度,至于右边的那个积分其实就是简单的质量乘以加速度
拉力和加速度都是矢量,不过加速度可以看成只有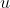 方向的分量 方向的分量
至于两个拉力,就没有这么幸运了,不过他们也有可以化简的关系
因为拉力是在端点切线方向,于是可以做分解而两个方向的比值正好是切线的斜率
于是可以得到两个分力的关系:
+T_x^2(x)=|\\mathbf{T}(x)|^2)
=T_x(x)\\frac{du}{dx})
所以有
=|\\mathbf{T}(x)|\\frac{du}{dx}/\\sqrt{(\\frac{du}{dx})^2+1)
因为 很小,所以分母直接看成1,于是得到 很小,所以分母直接看成1,于是得到
\\doteq|\\mathbf{T}(x)|\\frac{du}{dx})
\\doteq|\\mathbf{T}(x)|) (近似等.....干脆就等于得了 (近似等.....干脆就等于得了
对于加速度也可以同样处理,得到

对上面的方程写成分量方程
-T_u(x)=\\int_x^{x+\\Delta%C2%A0x}\\rho(x)a_udx) (*) (*)
-T_x(x)=\\int_x^{x+\\Delta%C2%A0x}\\rho(x)a_xdx)
实际上在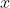 方向上,基本上没有加速度(很显然嘛,想想弦振动的方向 方向上,基本上没有加速度(很显然嘛,想想弦振动的方向
所以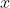 方向上的力是相等的,: 方向上的力是相等的,:
=T_x(x))
所以我们只须考虑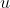 方向的情况,把方程(*)的左端变成一个积分: 方向的情况,把方程(*)的左端变成一个积分:
a_udx)
带入
dx=\\int_x^{x+\\Delta%C2%A0x}\\rho(x)a_udx)
记 为常量 为常量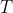 , ,
这样应该没问题吧...|)
dx=\\int_x^{x+\\Delta%C2%A0x}\\rho(x)a_udx)
两边求导
dx=\\rho(x)a_udx)
整理下
}\\frac{d^2u}{dx^2}=a_u)
因为加速度是位移的二阶导数

于是方程变成了
}\\frac{d^2u}{dx^2}=\\frac{d^2u}{dt^2})
吉他的弦粗细目测是均匀的,所以密度应该是个常数,记为 ,弦的振动方程就出来了 ,弦的振动方程就出来了

加上边界条件:
=0,\\,u(l,t)=0)
再加上初始条件:
=\\begin{cases}\\frac{h}{x_0}x%20&%200%3Cx%3Cx_0%20\\\\\\frac{h}{l-x_0}(l-x)%20&%20x_0%3Cx%3Cl\\end{cases})

好吧,解吧.
用分离变量法来解这个方程(本来打算写的,实在写不动了..此处略去1000行,有兴趣的去找本数学物理方程看.(喂喂,你们根本都知道怎么解的吧!
得到方程的解
=\\sum_{n=1}^{\\infty}\\frac{2}{l}\\int_0^lu(\\xi,0)\\sin\\frac{n\\pi%C2%A0\\xi}{l}d\\xi\\cdot\\cos\\sqrt{\\frac{T}{\\rho}}\\frac{n\\pi%C2%A0t}{l}\\sin\\frac{n\\pi%C2%A0x}{l}) (为啥钻出个 (为啥钻出个 ?因为要和 ?因为要和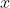 区别,实际上还是 区别,实际上还是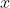 ,只是含 ,只是含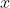 的项不能写进积分里喵.前面那坨积分是个定积分,是个常数,于是邪恶的用常数 的项不能写进积分里喵.前面那坨积分是个定积分,是个常数,于是邪恶的用常数 代替 代替
=\\sum_{n=1}^{\\infty}C_n\\cos\\sqrt{\\frac{T}{\\rho}}\\frac{n\\pi%C2%A0t}{l}\\sin\\frac{n\\pi%C2%A0x}{l})
这是个什么玩意儿?
这个玩意儿就是N个驻波的叠加
 (图片来自维基overtone (图片来自维基overtone
比如当 时这个驻波是 时这个驻波是

其中 为驻波项,是我们眼睛可能能看见的,空间上的波动 为驻波项,是我们眼睛可能能看见的,空间上的波动
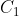 是眼睛能看到弦的最大振幅,也代表的声音的强度(其实很难看到,当然你使劲儿拨会看得比较清楚些 是眼睛能看到弦的最大振幅,也代表的声音的强度(其实很难看到,当然你使劲儿拨会看得比较清楚些
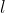 是眼睛看见弦振动的驻波波长 是眼睛看见弦振动的驻波波长
 为音频项,是耳朵听见的声音, 为音频项,是耳朵听见的声音,
声音频率(音调)是
那么泛音是什么呢?其实当[img][/img]1" src="http://www.codecogs.com/gif.latex?n%3E1">时,后面的声音都是泛音
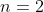 时声音频率是 时声音频率是 ,这就是第一泛音 ,这就是第一泛音
 时的声音就是第二泛音,以此类推. 时的声音就是第二泛音,以此类推.
细心的同学一定发现了方程的解其实是所有泛音的叠加,
但是平时只能听到第零泛音(有这种说法么?就是拨弦听到的声音.
这是因为[img][/img]C_2>C_3..." src="http://www.codecogs.com/gif.latex?C_1%3EC_2%3EC_3...">
第零泛音的声音比第一第二第n泛音的声音都大,把他们都盖住了.
所以要弹第一泛音,就要减少振幅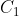 同时尽量保持振幅 同时尽量保持振幅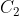
参考上面的驻波图,弹第一泛音就需要在弦的二分之一处制音以压制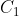 保持 保持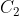
第二泛音在弦四分之一处制音,压制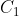 和 和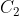 保持 保持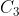
更高的泛音就很难控制了,因为它们的振幅实在太小,很难再把低频的音给制住
如果有蛋疼的人可以把 积分出来,然后画个图,看看各个泛音能有多大. 积分出来,然后画个图,看看各个泛音能有多大.
我比较懒,就猜猜,应该比较接近一个伽玛分布吧(揍
参考文献:
谁便找一本<数学物理方程>
<小林克己 初级>
维基百科(还去查了分部积分,太丢脸了...
感谢你看完
|
|